パラドックスという言葉の意味は何となく聞いたことはあるものの、どんなものがあるのかいまいちピンと来ていないという人は多いのではないでしょうか。
今回はそんな「パラドックス」について焦点を当て、有名なパラドックスを16個紹介していきます。豆知識の一つとして覚えていってもらえれば幸いです。ぜひ最後まで読んでいってみてください。
それではさっそく参りましょう。
パラドックスとは?
パラドックスとは、逆説やジレンマ、矛盾という意味を持っています。
逆説,あるいはパラドックスとは、正しい,あるいは一見正しく見える前提からおかしな結論が導きだされてしまうことです。前提や,途中の考え方がまちがっていたり,あるいは、パラドックスそのものはまったく正しいのに,結論をおかしいと思う私たちの直感がまちがっているということもあります。パラドックスは,言葉や数字、論理といった実体のないものもあれば,経済学や物理学などの分野で現実に確認されているものもあります。
引用:パラドックス大図鑑
パラドックスとは、見かけで判断する真偽が、事実の真偽とは反対であることという意味合いを持ちます。
簡単に言うのならば、「間違っているように見えて、実は正しい」。それがパラドックスということになります。

パラドックスの概要がなんとなくわかったところで、実例といきましょう!
知っておきたい有名なパラドックス16選
それでは、知っておきたい有名なパラドックスを16個紹介していきます。面白いなと思ったパラドックスが一つでもあれば幸いです。自分の知識の一つに加えるのはもちろんのこと、話のネタの一つにでもしていただけたらと思います。
探求のパラドックス

探求のパラドックス。
探求の対象が何であるかを知っていなければ探求はできない。さもなくばそれは顔も名前も知らない人を探すようなものである。しかしその対象を知っていればそもそも探求する必要がないというパラドックスです。
探求する対象Xを知らないのであれば、Xをどのような方法・目処で探求すればよいのかわかりません。仮にXらしきものに到達したとしても、それが本当にXなのかを確かめるすべがありません。そして探求する対象Xを知っているのであれば、そもそもXについて探求する必要がなくなってしまいます。
この二つの背理によって探求の必要性に疑問を投げかけているのが、探求のパラドックスです。

ちょっと難しいか。。
男か女かのパラドックス
男か女かのパラドックス。
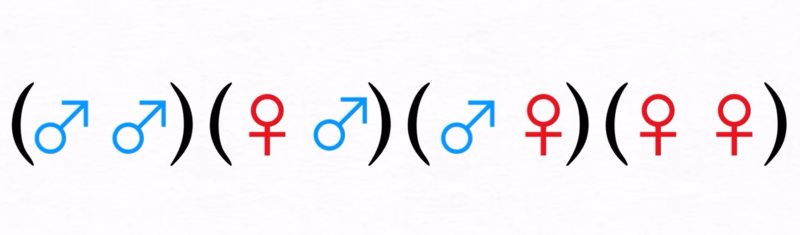
ある家庭に2人の子どもがいる。そのうちの1人が男の子であることが分かっているとき、もう1人も男の子である確率はいくらか?
という確率のクイズを考えてみましょう。このクイズの回答として、
- 1人が男の子であることと、もう1人の子の性別は独立なので確率は1/2
- 子ども2人の性別は(男、男)(女、男)(男、女)(女、女)の4通りある。1人が男の子なのであり得るのは(男、男)(女、男)(男、女)の3通りで、そのうちもう1人も男の子なのは1通りなので確率は1/3
という2つの回答があり、このクイズではどちらが正しいのかが議論になる。混乱をもたらす原因は問題文が、
- ある特定の1人が男の子だと分かった時のもう1人が男の子である確率を問う問題
- 少なくとも1人が男の子だと分かった時の2人とも男の子である確率を問う問題
という2通りの解釈ができてしまうことにあります。前者で解釈すれば1/2が正しくなり、後者で解釈すれば1/3が正しくなるのです。これが男か女かのパラドックス。
アキレスと亀

アキレスと亀。「アキレスが亀に追いつく位置より前では、絶対に追い越せない」
「アキレスと亀」は数学的な無限分割が不可能と考えたゼノンのパラドックスのことです。
- アキレスが追って1地点を出発するころ、亀はすでに先の2地点にいる
- その2地点にアキレスが到着するまでに、亀はさらに少し先の3地点に着いている
- アキレスがその3地点に着くころには、亀の方はすでに4地点にいる
このように、両者の距離は縮まっているが、アキレスが亀に追いつくことはないというパラドックスです。

個人的に結構頭を使った話で面白かった。
親殺しのパラドックス
親殺しのパラドックス。
「ある人が時間を遡って、血のつながった祖父を祖母に出会う前に殺してしまったらどうなるのか」というものを考えていく際に生じるパラドックスです。
その場合、その時間旅行者の両親のどちらかが生まれてこないことになり、結果として本人も生まれてこないことになります。したがって、存在しないものが時間を遡る旅行もできないことになり、祖父を殺すこともできないから祖父は死なずに祖母と出会う。すると、やはり彼はタイムトラベルをして祖父を殺す。。このように堂々巡りになるという論理的パラドックスになります。
ちなみにこのパラドックスは、時間に逆行するタイムトラベルが不可能だとする証拠として使われてきたといいます。一方で、パラドックスを避けるための様々な仮説も提案されてきました。例えば、過去は決して改変できないという考え方では、祖父や親を殺そうとしてもその試みは失敗し、相手は必ず生き延びようとする。あるいは、過去へのタイムトラベルは別の時間線を生み出すだけで、その時間旅行者が生まれた時間線はそのまま残っているという考え方もあります。
このパラドックスの考え方もあり、現在までの物理学の研究において、未来にいく方法は見つかっているが、過去に行く方法は未だ見つかっていないといいます。

タイムマシーンの実現にはまだまだ時間がかかりそう。。そもそもできるのだろうか。
倹約のパラドックス

倹約のパラドックス。
倹約のパラドックスとは、不景気化の倹約による景気悪化のことを指します。
景気が悪くなると多くの人が対策として倹約をするが、その結果として需要が減って企業業績が悪化し、さらに景気が悪くなる状態のことを指します。
- みんな貯金ばかりするから消費が減る
- 消費が減れば企業は儲からない
- 新規事業などへの投資が減る
- 投資が減って経済が成長しなくなる
具体的には、個人や企業の貯蓄が増えると、その分消費が減少します。消費が減少すると企業の売上や利益が減少し、投資が減少します。投資が減少すると経済成長が低下します。これがループしてしまうというもの。
一般に不景気下において、無駄遣いしないように努める「倹約」という行動は家計防衛としては正しいとされています。しかしその正しい行動が、さらに事態を悪化させるというのが倹約のパラドックスになります。
満場一致のパラドックス

満場一致のパラドックス。
満場一致のパラドックスとは、「全員同じ意見は逆に信用できない」というものです。
クラスで出し物をする場合に、「お化け屋敷」「喫茶店」「メイドカフェ」の3つに意見が絞られた。
40人いるクラスで、全員が口裏合わせなど無しに「お化け屋敷」を選択した場合、逆にその意見の信頼が下がる。
例えば上記のような例を挙げると、全員が口裏合わせなどなしに「お化け屋敷」を選択した場合、逆にその意見の信頼が下がるという現象が起きてしまいます。
人間の意見は必ずと言っていいほど、同じような選択肢を選ぶときは意見がばらける物であり、満場一致の意見が出てしまうと人間は直感的に違和感を感じてしまうのです。
このようなことから、多数決を行う場合には満場一致のパラドックスに気を付ける必要があります。
抜き打ちテストのパラドックス
抜き打ちテストのパラドックス。
「未来の予測できないときに起こるが、いつまでに起きるかという期限は決まっている」という事柄は、「いつまでに起きるかという期限は決まっている」という制限の存在によって、「そもそも予測できないときに起こる事象」と言えなくなるのではないか?というものです。
例として、ある教師が学生たちの前で次のように予告しました。
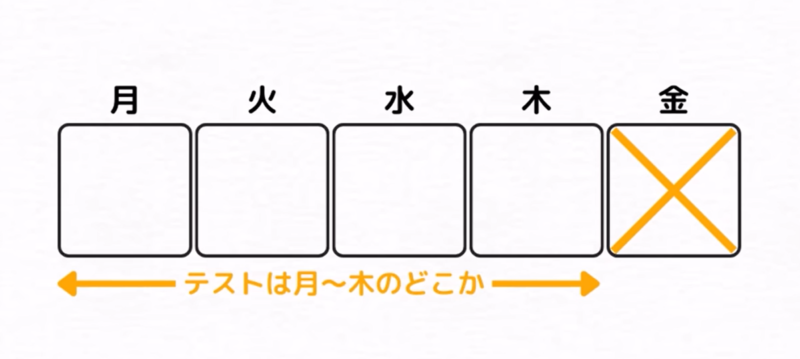
来週の月曜日から金曜日までのいずれかの日にテストを1回行う。抜き打ちでテストであり、テストが行われる日がいつかはわからない。
これを聞いたある学生は、以下の推論の結果「抜き打ちテストは不可能である」という結論に達しました。
①まず、金曜日に抜き打ちテストがあると仮定する。すると、月曜日から木曜日まで抜き打ちテストがないことになるから、木曜日の夜の時点で、翌日(金曜日)が抜き打ちテストの日であると予測出来てしまう。これでは抜き打ちとは言えないので金曜日には抜き打ちテストができないということが分かる。
②次に、木曜日に抜き打ちテストがあると仮定する。すると、月曜日から木曜日まで抜き打ちテストがないことになるから、水曜日の夜の時点で木曜日か金曜日のどちらかの日に抜き打ちテストがあることが予測できるが、①により金曜日には抜き打ちテストがないことがすでに分かっているので、翌日(木曜日)が抜き打ちテストの日であると予測出来てしまう。よって、木曜日にも抜き打ちテストを行うことができないということが分かる。
③以下同様に推論していくと、水曜日、火曜日、月曜日にも抜き打ちテストを行うことができないということが分かる。したがって、ただの屁理屈に聞こえるが「先生はいずれの日にも抜き打ちテストを行うことができない」という結論になる。
この話にはオチがあります。結論付けた学生でしたが、翌週、テストは水曜日に行われました。屁理屈推論をしたにもかかわらず、学生はまったくテストの日を予測できなかったのでした。
このパラドックスは、「教師の宣言を信じれば不整合になり、信じなければ誤った事柄を信じることになる」という構造を持っています。
教師の「来週の月曜日から金曜日までのいずれかの日にテストを1回行う。抜き打ちテストであり、テストが行われる日がいつかはわからない。」という宣言は、次の二つの命題に分割できます。
- 予告した期間(来週の月曜日から金曜日)のいずれかの日に必ずテストを実施する。
- 学生が推論によって予測できる日には、テストを実施しない。
また、教師が「明日、抜き打ちテストを行う」と発言した場合、このパラドックスを良くあらわす発言をしたことになります。

ちょっと複雑だけど、これも結構面白かった。
嘘つきのパラドックス

嘘つきのパラドックス。
嘘つきのパラドックスの一例として、エピメニデスのパラドックス(紀元前600年ごろ)があります。
クレタ人であるエピメニデスが「クレタ人はいつも嘘をつく」と言った場合、クレタ人が本当にいつも嘘をつくなら、彼のこの言葉も嘘となり、クレタ人はいつも嘘をつかないことになってしまう、というのがエピメニデスのパラドックスです。
嘘つきは誠実に嘘をつき続けることが前提で成り立っているパラドックスとなっています。

これはシンプルで面白い。
ヘンペルのカラス

ヘンペルのカラス。
このパラドックスはすべてのカラスは黒いということを証明する際に発生するものです。
このことを数学で言う対偶論法で証明するならば、「全てのカラスは黒い」という命題はその対偶「全ての黒くないものはカラスでない」と同値であるので、これを証明すればいいということになります。
そして「全ての黒くないものはカラスでない」という命題は、世界中の黒くないものを順に調べ、それらの中に一つもカラスがないことをチェックすれば証明することができます。
つまり、カラスを一羽も調べること無く、それが事実に合致することを証明できるのです。
これは日常的な感覚からすれば奇妙にも見え、この奇妙さが、ヘンペルのカラスのパラドックスです。
モンティホール問題

モンティホール問題。これは、確率論の反直感的な性質を示す有名な問題と言います。
「直感と計算が異なるときあなたならどちらを選ぶか」ということが問われます。
問題の概要としては、3つの扉「A、B、C」から豪華景品である高級車が入っている扉を当てるゲームを考えてみてほしい。
1つの扉には車があり、残りの2つの扉は何も入っていないハズレの扉である。
→つまり当たる確率は1/3である
実際のやり取りを見てみよう。
まず回答者をBの扉を選びます。すると扉の中身をすべて把握している司会者が、「それではここで選ばれなかった2つの扉のうち、ハズレの扉をひとつ開けてみましょう。」
そう言うと司会者はAの扉を開けて見せ、回答者にハズレの扉であることを確認させました。
そして司会者は続けて言います。「つまり、あなたが選んだBの扉か、残ったCの扉のどちらかに車がるということですね。」と。「残った扉は2つですから、あなたの選んだ扉に車がある確率は1/2になりました。」「特別にこの2つの扉で、どちらに車が入っているのか選びなおすチャンスを与えましょう。」
このように言われた場合、多くの参加者は自分の選択を変更しませんでした。
それは扉を変更してもしなかったとしてもどちらも確率は1/2のように思えるからです。しかし実際には、扉を変更したほうが当たる確率が2倍になるというのが、モンティホール問題のパラドックスです。
では仮にAの扉が当たりであると仮定して、扉を変更する場合と変更しない場合を考えてみましょう。
まず扉を変更しない場合は、単純にAを選べば当たり、B、Cを選べばハズレとなり、確率は1/3となります。
次に扉を変更する場合と考えてみます。最初にAの扉を選んだ場合、残りにB、Cの扉のどちらかがオープンされます。
そして選ばれなかったもう一方の扉にチェンジすることになるため、結果的にハズレを選ぶことになります。Bの扉を最初に選んだ場合、ハズレであるCの扉がオープンされるため、当たりであるAの扉にチェンジすることとなります。
つまり、Bの扉を選んでからチェンジすれば、必ず当たりを引くことになるわけです。
Cの扉を選んだ時も同様に、ハズレであるBの扉がオープンされるため、当たりであるAの扉にチェンジすることになります。つまり選んだ扉をチェンジする場合、最初にAの扉を選ぶとハズレになり、B、Cの扉を選ぶと当たりになります。
このように、当たる確率が2/3となるわけです。
つまり、最終的には扉をチェンジしない場合は当たりを引く確率は1/3となり、扉をチェンジする場合は2/3ということになるのです。そのため結果的には、選んだ扉をチェンジしたほうが当たる確率は2倍になるのです。
このように人間の直感的な答えと、計算で導き出した答えがかけ離れていることがモンティホール問題の特徴であり、これは数学の確率問題である「条件付き確率」にも通ずるものがあると言われています。
テセウスの船

テセウスの船。
その昔、ギリシャの英雄テセウスという人が船を所有していました。その船は経年劣化で部品が痛んできたため、壊れた部品は徐々に新しいものを交換されていきました。
そして、最終的には船の全ての部品が交換され、元の部品は一つも残っていない状態になってしまいました。
では果たして、すべての部品が交換された後の船は、最初のテセウスの船と同じ船と言えるのだろうか?
これがテセウスの船のパラドックスとなります。
これは私たちが、完全に復元された城などを見たときに、「これって当時からの城じゃないよね?」と感じるのと同じようなものと言えます。
シュレディンガーの猫

シュレディンガーの猫。
ある加工された一つの箱がありました。
その箱の中に猫1匹と、「50%の確率で爆発する爆弾」を入れたとします。
この箱は完全に密閉、防音加工が施されていて、箱を開けてみるまで爆弾が爆発してしまったかどうかは一切わかりません。
このとき、この箱の中には爆弾が爆発して猫が死亡している可能性と、爆発せずに猫が生きている可能性がそれぞれ50%ずつ存在しています。
ここで問題が生じます。猫の生死が確定してしまうのは一体いつなのでしょうか?
それは箱を開けてみないと分かりません。つまり箱がとじている間は「猫が生きている」とも「猫が死んでいる」ともいえない状態ということになるのです。
世界中の量子力学者によると、私たちがこの箱を開けてみるまで、猫は生きている状態と死んでいる状態を重ねて存在しているということになるとのこと。
このように2つの状態が重なり合っていることがシュレディンガーの猫のパラドックスです。
また、かの有名はアインシュタインは「観測するまで答えはわからず確率でしか言えないが、正解は最初からこの世界に存在している」という意見を残しています。
全能の逆説

全能の逆説。
まず、全能の神がいると仮定し、その神は宇宙を創ることも、時間を操ることも何でもできるとします。
その神が、「自身がもち上げられないほどの岩を作ることができるのか?」と問いてみます。
考えうる回答として2つのパターンがあります。
- 神が「自身がもち上げることのできない岩」を作ることができるのであれば、岩を作れたとしても持ち上げることができないので、その神は全能ではない。
- 神が「自身がもち上げることのできない岩」を作ることができないのならば、岩が作れないとしてその神は全能ではなくなる。
よって、どちらにせよ神の全能を否定することになります。これが全能の逆説です。
ワニのパラドックス

ワニのパラドックス。
ある日、沼地で人食いワニが親子の前に現れ子どもを人質に取りました。
そしてワニは母親に「自分がこれから何をするか言い当てられたら子どもを食べないでやろう。しかし間違えた場合は子供を食う。」と母親に言いました。
母親は少し考えた後、「あなたはその子を食べるでしょう。」と答えました。
するとどうでしょう。ここで不可解なことが起こります。
選択肢としては、
- ワニが子どもを食べようとした場合、母親に何をするか充てられたことになり子どもを食べることができない。
- 逆に子供を食べようとしないでいると、母親の予想は外れたことになりワニは子供を食べようとするが、それだと母親の予想は当たったことになり、1.へと戻ってしまう。
という2通りが考えられます。このように1と2を無限にループし、結果的にワニは子供を食べることも食べまいとすることもできなくなってしまうという訳です。
ワニが自分が設定したルールによって自己矛盾に陥ってしまうというのが、ワニのパラドックスであります。

ワニがもどかしい様子を想像してしまった(笑)
ハゲ頭のパラドックス
ハゲ頭のパラドックス。
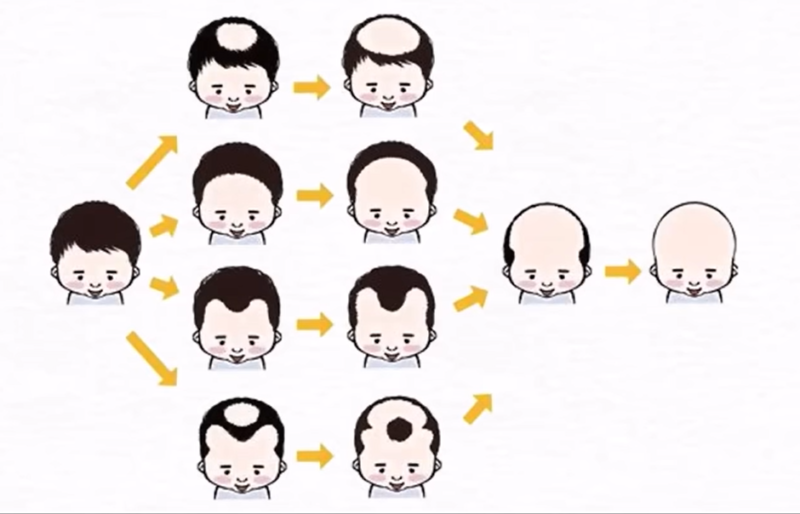
髪の毛が1本もない人がいたとします。その人は誰がどう見てもハゲである。
そこで、そのハゲの人に髪の毛を1本足したとしてもその人が依然としてハゲであることは変わりません。
このまま髪の毛を足していってフサフサになったとしても、その人がハゲなことに変わりはない。
つまり全人類がハゲているといえるのである。というのがハゲ頭のパラドックスです。
このパラドックスは「ハゲ」の基準が具体的に決められていないことから生じている問題でもあり、類似問題として「砂山から砂粒を1つずつ取り、最後の1粒になったとしても、それは砂山と言えるのか?」という砂山もパラドックスというものもあります。

全人類がハゲは哲学すぎる。
悪魔の証明

悪魔の証明。
悪魔の証明とは、主に「証明できないもの」のことを指します。別名を未知証明とも言います。
例えば、「ツチノコが存在することを証明しろ」という命題であれば、ツチノコを一匹発見するだけでそれを証明できます。
では逆に「ツチノコがいないことの証明」であればどうでしょうか?
この「いないことの証明」というのは困難、もしくは不可能だといいます。
なぜなら、世界中でたまたま誰も見ていないだけかもしれないし、海底や、宇宙の隅々まで調べることはほぼ不可能だからです。
このように悪魔の証明である「ないことの証明」は、考えられる可能性の全てをつぶす必要があるため、不可能に近いものであることが分かります。
おわりに
最後までお読みいただきありがとうございました。今回は知っておきたい有名なパラドックスを16つ紹介してきました。知っているもの、今回初めて知って参考になったところはありましたでしょうか。
最後にまとめてざっと紹介します。
- 探求のパラドックス
- 男か女かのパラドックス
- アキレスと亀
- 親殺しのパラドックス
- 倹約のパラドックス
- 満場一致のパラドックス
- 抜き打ちテストのパラドックス
- 嘘つきのパラドックス
- ヘンペルのカラス
- モンティホール問題
- テセウスの船
- シュレディンガーの猫
- 全能の逆説
- ワニのパラドックス
- ハゲ頭のパラドックス
- 悪魔の証明
紹介してきて、個人的におすすめ?(面白いなと思ったパラドックス)は「アキレスと亀」「モンティホール問題」「テセウスの船」「ワニのパラドックス」「ハゲ頭のパラドックス」「悪魔の証明」です。どれも、なるほどなぁと唸る内容でした(笑)
パラドックスの知識自体が、仕事やプライベートで役に立つことはないかもしれませんが、豆知識の一つとして知っておくだけでも自分自身の引き出しの懐が広くなるかもしれません。
個人的にこういった頭を使って考えるお話が好きで面白いと思ったので、今回は紹介させていただきました。またこういった小難しい面白いものを見つけたら紹介していきたいです。
毛が何本になったら「ハゲ」なのだろうか?(真剣に議論したい()?)
ではまた。
参考動画はコチラ↓












コメント